wykaż, że.. annk343: W trójkącie ABC długości boków wynoszą : AB = c, AC = b, BC = a, gdzie 0<a<b<c. Pole tego trójkąta wynosi 3. Wykaż, że AC> √6 . Proszę o odpowiedź

Beztroski:

	abc
Wychodząc z wzoru P=
	4R

Oraz korzystając "po drodze" z wzorów:

a		b		c
	=		=		=2R
sinα		sinβ		sinγ

	sin(β)
Otrzymujemy: b=√2P(		)0,5
	sinαsinγ

β i α ∊(0^o;90^o)⋁β>α (większy kąt leży na przeciwko większego boku)

	sinβ		sinβ
Więc		>1,a		:sinγ" tym bardziej">1
	sinα		sinα

Skoro √2P=√6 to b>√6 [ P=3 ]

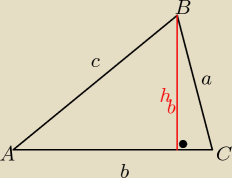Eta: Prościej tak 0<a<b<c , |AC|= b

	b*h
P=		= 3
	2

	6
to: h=		.... i h < a
	b

	6
		<a <b
	b

	6
		<b
	b

to: b²>6 => b> √6 |AC| >√6 c.n.u